
(This also holds for the cosine function.) The period of the function y = sin Cx is 2π/|C|. The additional factor C in the function y = sin Cx allows for period variation (length of cycle) of the sine function. The minimum value is 4 − 3 = 1 (Figure 6 ). What are the maximum and minimum values of the function? The minimum value is 1 −2 = −1 (Figure 5 ).Įxample 2: Graph the function y = 4 + 3 sin x. This minimum occurs whenever sin x = −1 or cos x = −1.Įxample 1: Graph the function y = 1 + 2 sin x. The minimum value of the function is m = A ‐ |B|. This maximum value occurs whenever sin x = 1 or cos x = 1.
The maximum value of the function is M = A + |B|. These two functions have minimum and maximum values as defined by the following formulas. This also holds for the cosine function (Figure 4 ).Įxamples of several amplitudes of the sine function.Ĭombining these figures yields the functions y = A + B sin x and also y = A + B cos x. The amplitude, | B |, is the maximum deviation from the x‐axis-that is, one half the difference between the maximum and minimum values of the graph. The additional factor B in the function y = B sin x allows for amplitude variation of the sine function. This also holds for the cosine function (Figure 3 ).Įxamples of several vertical shifts of the sine function. The additional term A in the function y = A + sin x allows for a vertical shift in the graph of the sine functions. Several additional terms and factors can be added to the sine and cosine functions, which modify their shapes. Multiple periods of the a) sine function and b) cosine function. The sine function and the cosine function have periods of 2π therefore, the patterns illustrated in Figure are repeated to the left and right continuously (Figure 2 ). One period of the a) sine function and b) cosine function. Next, plot these values and obtain the basic graphs of the sine and cosine function (Figure 1 ). To see how the sine and cosine functions are graphed, use a calculator, a computer, or a set of trigonometry tables to determine the values of the sine and cosine functions for a number of different degree (or radian) measures (see Table 1).

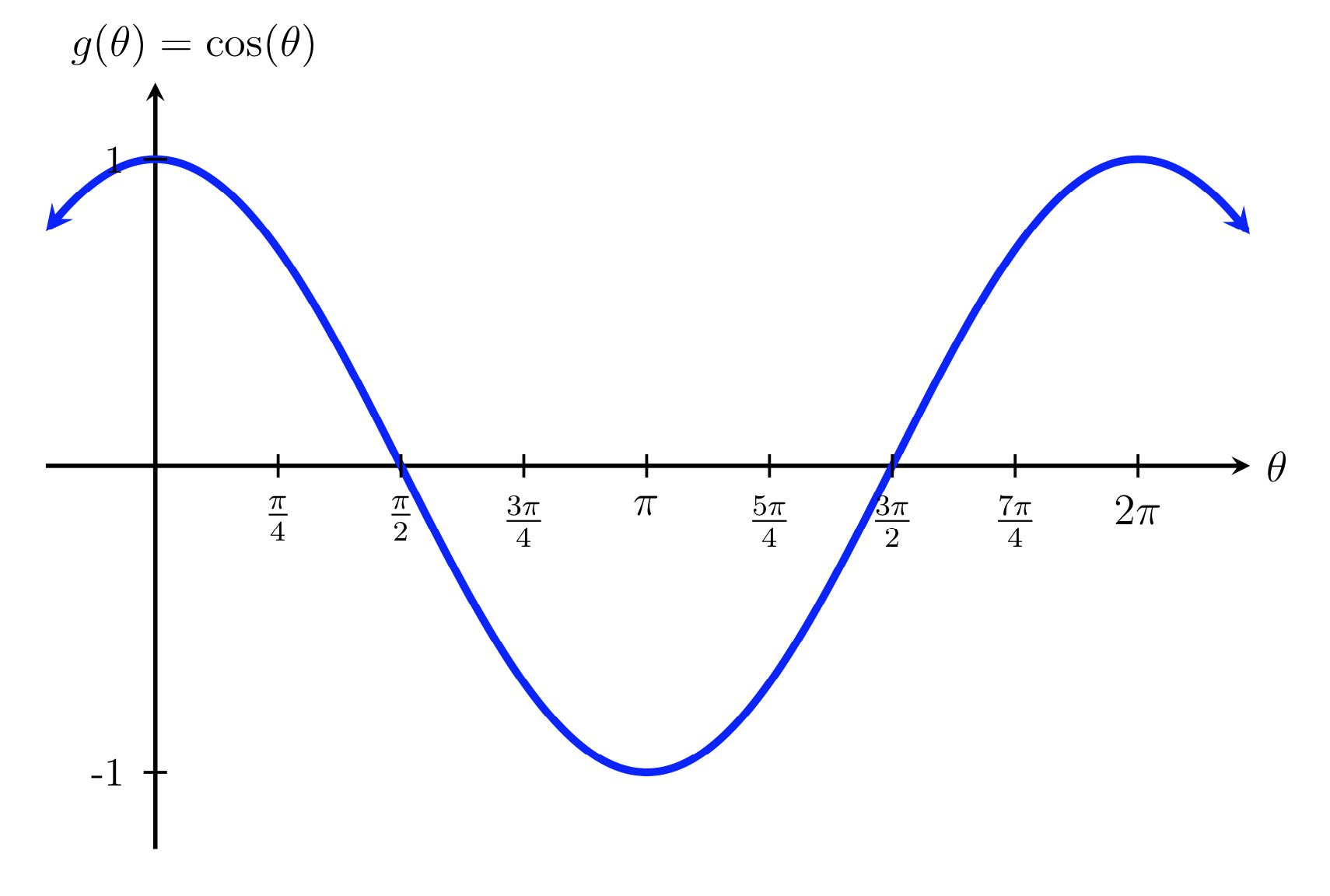
We will see that the same techniques we used to graph functions in algebra, like parabolas and absolute value functions, can be applied to how we transform and translate trigonometric functions, as nicely stated by Purple Math. In this video we will discover how to identify all the major component of a sine and cosine graph, and learn an awesome pattern or technique for graphing these periodic functions to make is quick and easy! Besides, we would miss out on being able to visualize what a sine or cosine function actually does as it travels around the unit circle. Well, it’s no fun to be stuck running around a circle forever – it’s much easier for us to stretch our legs and graph each function along the Cartesian Plane (x-y-axes). This is due to the fact that as we move around the unit circle in a counterclockwise fashion, we notice that the largest value for sine or cosine is 1, therefore it’s amplitude (height) is also 1, as nicely shown by Khan Academy. When we look at the graph that is generated by unwrapping our unit circle, we will see that it generates a wave-like graph, where the domain is all real numbers and the range is between -1 and 1.

Visualizing the Amplitude of the Sine Function

Well, a function that is indeed periodic, is one that repeats forever at regular intervals – just like the waves/tide in the ocean. All trigonometric functions are periodic! In doing so, we will plot these point on an xy-plane and see what it creates. Then we’re going to take our handy-dandy Unit Circle and create a table of values from all the radian measures and ordered pairs. In order to see how this works, we are first going to let our theta become the variable x, so it’s easier for us to apply it to basic graphing techniques. Well, that’s exactly what we’re about to do because we’re going to Graph Sine and Cosine!īecause we are now using Radian measure to represent angles, we are able to treat our circular function (i.e., sine, cosine, tangent, etc.) like any other function with a domain or real numbers! Would it shock you if I told you that we are now going to take everything we know (triangles stuck in a Unit Circle) and unwrap it so that we can see it graphed out on the coordinate plane like any other function? We are now pretty comfortable with our Unit Circle and our six trigonometric functions.


 0 kommentar(er)
0 kommentar(er)
